• 목록

연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화

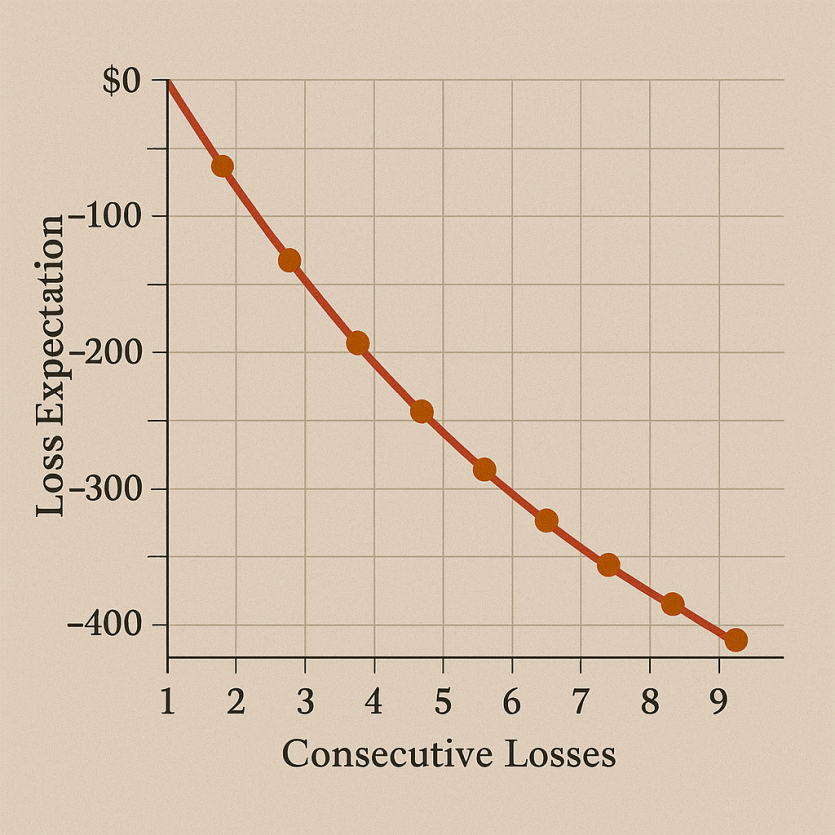
카지노 게임을 이해할 때 가장 중요하지만 자주 간과되는 개념 중 하나는 **연패(lose streak)**가 가지는 수학적 의미입니다. 우리는 종종 "이제쯤 이길 차례야"라는 막연한 기대를 가지고 배팅을 확대하지만, 연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화라는 관점에서 보면 이는 매우 위험한 착각입니다.

이 글은 베팅 시스템별로 연패가 발생했을 때 기대 손실(EV)의 누적이 어떤 식으로 진행되는지 시각화하고, 이를 기반으로 실제 자금 리스크를 어떻게 관리할 수 있는지를 설명합니다. 수학적으로 접근한 이 분석은 베팅 시스템의 본질을 직관적으로 이해하는 데 큰 도움이 될 것입니다.

1. 연속 연패 시 손실 기대값의 기본 개념

기대값(Expected Value)은 장기적인 손익 평균을 의미하며, 연패가 발생할 경우 손실은 단순히 연속된 패배 수만큼 누적됩니다.

예: RTP 96% 슬롯의 단일 베팅 기대값은 –0.04
10연패 시 손실 기대값: 10 × –0.04 = –0.40

이처럼 연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화에서 핵심이 되는 것은 베팅 방식에 따라 이 곡선이 얼마나 급격하게 변하는가입니다.

2. 고정 베팅 시스템: 선형 리스크 구조

연패 횟수 누적 손실 기대값 ($)

1 –0.04
5 –0.20
10 –0.40
20 –0.80

고정 베팅은 같은 금액을 반복하므로 선형 증가를 보입니다.

예측 가능성이 높고, 리스크 관리가 쉬운 시스템입니다.

3. 마틴게일 시스템: 기하급수적 리스크 확대

연패 횟수 베팅 순서($) 누적 베팅 합계($) 누적 손실 기대값($)

1 1 1 –0.04
2 1 → 2 3 –0.12
3 1 → 2 → 4 7 –0.28
5 ... 31 –1.24
10 ... 1023 –40.92

연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화를 통해 보면 마틴게일은 매우 가파른 상승 곡선을 그립니다.

자금이 많지 않다면 극단적인 리스크가 따릅니다.

4. 피보나치 시스템: 완만한 곡선, 중간 리스크

연패 횟수 베팅 합계($) 누적 손실 기대값($)

1 1 –0.04
3 4 –0.16
6 20 –0.80
10 143 –5.72

상승 곡선이지만 마틴게일보다는 느립니다.

연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화에서 ‘절충형 전략’의 대표 예시입니다.

5. 그래프 비교 요약

EV($)
 |\
 | \
 |  \          (고정 베팅: 선형)
 |  \

EV($)
 |        /
 |      /          (피보나치: 완만한 곡선)
 |    /

EV($)
 |            /
 |        /              (마틴게일: 급격한 상승)
 |    /

6. 연패 확률 자체도 매우 현실적이다

슬롯 승률 20% 기준: 10연패 확률 ≈ 10.7%
마틴게일 5연패(승률 50%) 확률 = 3.125%

수백 번의 게임이 있는 카지노 환경에선 흔히 발생할 수 있는 수치입니다.

7. 실전 전략: 리스크에 맞는 시스템 선택

시스템 장점 단점 추천 대상

고정 베팅 손실 예측 가능 느린 회수 속도 초보자, 장기 안정형
마틴게일 빠른 손실 회복 가능 자금 붕괴 위험, 연패 취약 하이롤러, 짧은 게임 선호자
피보나치 중간 리스크, 감정 통제 유리 회수 속도 느림 전략적 베팅을 원하는 중급자 이상

8. 전문가 조언: 수학 기반 베팅 설계의 중요성

감정이 아닌 수학이 베팅을 지배해야 합니다.
연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화를 통해 자신에게 맞는 리스크 허용 범위를 정해야 합니다.
RTP, EV, 분산을 통합적으로 고려할 수 있어야 실제 베팅 전략이 실효성을 가집니다.

요약: 핵심 인사이트

연패는 확률적으로 자주 일어납니다.

마틴게일은 빠르지만 위험, 고정 베팅은 느리지만 안전
피보나치는 두 시스템의 중간 절충형

연속 연패 시 손실 기대값 그래프: 베팅 시스템의 수학적 리스크 시각화는 필수 도구입니다.

FAQ

Q. 연패 시 심리적으로 어떻게 대처해야 하나요?

A. 사전 설정된 베팅 시스템을 따르면 감정 개입을 줄일 수 있습니다.

Q. 피보나치는 가장 안전한가요?

A. 마틴게일보다는 안전하지만, 자금 관리와 커트라인 설정이 중요합니다.

Q. 어떤 게임이 연패에 덜 취약한가요?

A. 블랙잭, 바카라 뱅커 베팅 등 저분산 구조가 연패 방어에 유리합니다.


#연패기대값, #마틴게일손실, #베팅시뮬레이션, #슬롯연패, #피보나치베팅, #고정베팅안전성, #분산그래프, #EV그래프, #도박리스크관리, #카지노수학모델